Vexoben
Oct 31, 2017
SDOI2010地精部落
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=1925
看到全排列第一反应是状压DP,但是数据范围显然不允许。感觉到全排列个数的增加对答案的贡献有一些共性但是不知道怎么利用就看了一发题解。
对于前i个数,不必关心每个数具体是多少,只需知道相对大小即可。
设 f(i,j) 表示前i个数的排列中,第一个数是第 j 大,且a1>a2的方案数, g(i,j) 表示前i个数的排列中,第一个数是第 j 大,且a1<a2的方案数。
显然有 f(1,1)=g(1,2)=1;
向 f(i,j) 转移的时候,只关心相对大小,于是假设前i个数分别是1-i,将j放在第一个位置后,我们将大于j的所有数-1,这样我们就得到了[1,i-1]这些数可选,且开头要求升序排列,那不就是:
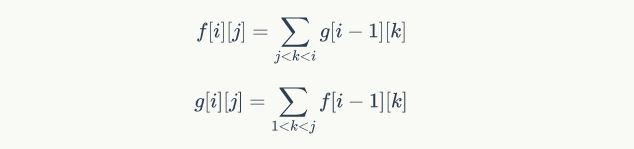
加个前缀和优化O(1)转移就能过了。
事实上也可以把g数组消去变成:f[i][j]=f[i-1][i-j+1]+f[i][j-1],计算答案把f[n]加起来乘2即可。
#include<bits/stdc++.h>
using namespace std;
const int N=4205;
int n,mod;
int f[2][N];
inline int Add(int x,int y)
{
return x+y>=mod?x+y-mod:x+y;
}
int main()
{
scanf("%d%d",&n,&mod);
int now=1,last=0;
for (int i=1;i<=n;i++) f[last][i]=1;
for (int i=2;i<=n;i++)
{
int sum=0;
memset(f[now],0,sizeof(f[now]));
for (int j=2;j<=n;j++)
{
sum=Add(sum,f[last][i-j+1]);
f[now][j]=sum;
}
swap(now,last);
}
int ans=0;
for (int i=1;i<=n;i++)
ans=Add(ans,f[last][i]);
ans=ans*2%mod;
printf("%d",ans);
return 0;
}
HDU4055 Number String
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4055
上一题利用到了波动排列的对称性质,这一题规定了每个位置的升降情况就需要稍微变一下
设f[i][j]表示前i个数的排列,最后一个数是第j大的方案数
于是有:
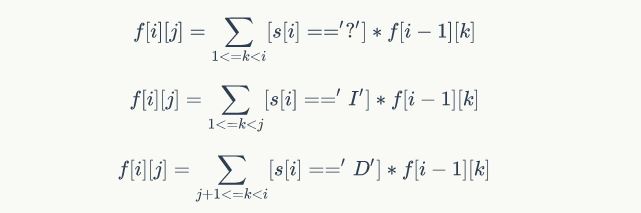
#include<bits/stdc++.h>
using namespace std;
const int N=1020;
const int mod=1000000007;
int n,m,f[N][N],sum[N];
char s[N];
inline int Add(int x,int y)
{
return x+y>=mod?x+y-mod:x+y;
}
inline int Sub(int x,int y)
{
return x<y?x-y+mod:x-y;
}
int main()
{
while (~scanf("%s",s+1))
{
n=strlen(s+1);
f[1][5]=1;
sum[1]=1;
for (int i=2;i<=n+1;i++)
{
for (int j=1;j<=i;j++)
{
if (s[i-1]=='I') f[i][j]=sum[j-1];
else if (s[i-1]=='D') f[i][j]=Sub(sum[i-1],sum[j-1]);
else f[i][j]=sum[i-1];
}
memset(sum,0,sizeof(sum));
for (int j=1;j<=i;j++)
sum[j]=Add(sum[j-1],f[i][j]);
}
printf("%d\n",sum[n+1]);
memset(f,0,sizeof(f));
memset(sum,0,sizeof(sum));
}
return 0;
}