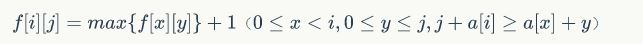Vexoben
Nov 10, 2017
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=3594
题解
先考虑DP:f[i][j][k]表示第i株玉米,用了j次拔高,第i株玉米高度为k的连续玉米数是多少,转移O(n),复杂度O(n^3*k)
注意到很明显的一个贪心:如果我们要拔高一列玉米,其右端点必然是最后一株玉米,因为如果不在最后一株玉米,我们将它移至最后一株玉米,将两株相连的费用不会增加。
换言之,拔高玉米只会对左端点的相对顺序产生影响。
所以压去k这一维,考虑f[i][j]表示前i株玉米,拔高j次连续玉米数是多少,显然第i株玉米一定被拔高了j次,则有:
复杂度O(n^2*k),并不会优化……
膜了一发题解,上述方程可以写成:
不妨在一次转移中将j+a[i]看做常数,那么可以转移到f[i][j]的是二维空间内满足.JPG)
用二维树状数组维护这个点集的最值即可,复杂度O(nlognk)
#include<bits/stdc++.h>
#define lowbit(x) (x&-x)
using namespace std;
const int N=1e4+501;
const int K=510;
int n,k,ans,a[N],tree[K][N],f[N][K];
inline int query(int x,int y)
{
int ans=0;
for (int i=x;i;i-=lowbit(i))
for (int j=y;j;j-=lowbit(j))
ans=max(ans,tree[i][j]);
return ans;
}
inline void updata(int x,int y,int num)
{
for (int i=x;i<K;i+=lowbit(i))
for (int j=y;j<N;j+=lowbit(j))
tree[i][j]=max(tree[i][j],num);
}
int main()
{
scanf("%d%d",&n,&k);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
for (int i=1;i<=n;i++)
for (int j=k;j>=0;j--)
{
f[i][j]=query(j+1,a[i]+j+1)+1;
updata(j+1,a[i]+j+1,f[i][j]);
ans=max(ans,f[i][j]);
}
printf("%d",ans);
return 0;
}