Vexoben
Dec 21, 2017
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=1001
题解
明显是求最小割。但点数1e6正解显然不是直接上网络流。
于是学习了一发s-t平面图的最小割.(2008集训队论文 周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》)
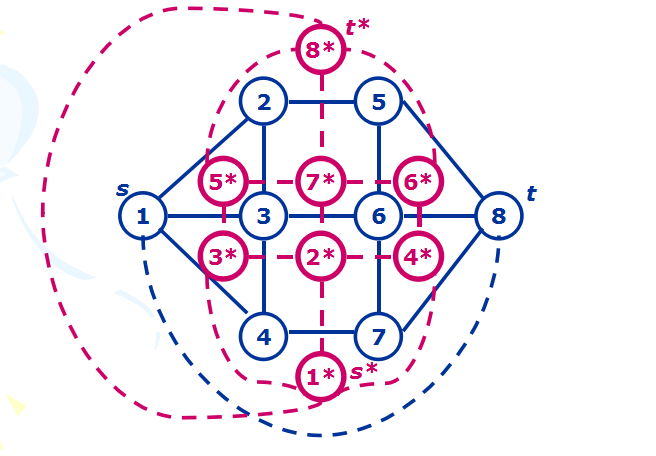
大致是将原平面图的每个面作为对偶图的一个点,每条边变为连接左右两个面的边,那么对偶图中的一个环就对应原图的一个割(相当于把几个点切下来)。给定源汇点后,在平面图从s向t连一条长为inf的边,这条边与原边会形成一个面,对应对偶图中的一个点。从这个面走到平面图的外面(即面积为inf的那个面),相当于平面图的一个割。对应到对偶图上,相当于两个面所对应点的路径。只需求出两个点之间的最短路,就得到了平面图的最小割。从而就可以在O((n+m)logn)的时间内解决这道题。
#pragma GCC optimize(2)
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<cstdio>
#include<time.h>
#include<vector>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
const int N=2e6+10;
const int M=6e6+10;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
int n,m,E,V,fir[N],dis[N],nex[M],arr[M],len[M],book[N];
struct pnt{
int u,dis;
bool operator < (const pnt &other) const {
return dis>other.dis;
}
};
priority_queue<pnt> q;
namespace FastIO {
template<typename tp> inline void read(tp &x) {
x=0; char c=getchar(); bool f=0;
for(;c<'0'||c>'9';f|=(c=='-'),c = getchar());
for(;c>='0'&&c<='9';x=(x<<3)+(x<<1)+c-'0',c = getchar());
if(f) x=-x;
}
template<typename tp> inline void write(tp x) {
if (x==0) return (void) (putchar('0'));
if (x<0) putchar('-'),x=-x;
int pr[20]; register int cnt=0;
for (;x;x/=10) pr[++cnt]=x%10;
while (cnt) putchar(pr[cnt--]+'0');
}
template<typename tp> inline void writeln(tp x) {
write(x);
putchar('\n');
}
}
using namespace FastIO;
void Add_Edge(int x,int y,int l) {
nex[++E]=fir[x];
fir[x]=E;
len[E]=l;
arr[E]=y;
}
inline void Init() {
read(n); read(m);
V=2*(n-1)*(m-1);
int x=1;
if (n==1||m==1) {
int ans=inf,l;
while (~scanf("%d",&l)) ans=min(ans,l);
printf("%d",ans);
exit(0);
}
for (int i=1;i<=n;i++)
for (int j=1;j<m;j++) {
int l; read(l);
if (i==1) Add_Edge(x,0,l),Add_Edge(0,x,l);
else if (i==n) Add_Edge(x,V+1,l),Add_Edge(V+1,x,l);
else Add_Edge(x,x-2*m+3,l),Add_Edge(x-2*m+3,x,l);
if (i==n-1&&j==m-1) x=2*(n-2)*(m-1)+2;
else x+=2;
}
x=2;
for (int i=1;i<n;i++)
for (int j=1;j<=m;j++) {
int l; read(l);
if (j==m) Add_Edge(x-1,0,l),Add_Edge(0,x-1,l);
else if (j==1) Add_Edge(x,V+1,l),Add_Edge(V+1,x,l);
else Add_Edge(x,x-3,l),Add_Edge(x-3,x,l);
if (j!=m-1) x+=2;
}
x=1;
for (int i=1;i<n;i++)
for (int j=1;j<m;j++) {
int l; read(l);
Add_Edge(x,x+1,l),Add_Edge(x+1,x,l);
x+=2;
}
}
inline void Dijkstra() {
memset(dis,0x3f,sizeof(dis));
dis[0]=0; q.push((pnt){0,0});
while (!q.empty()) {
register int u=q.top().u; q.pop();
if (book[u]) continue;
book[u]=1;
for (register int i=fir[u];i;i=nex[i])
if (dis[u]+len[i]<dis[arr[i]]) {
dis[arr[i]]=dis[u]+len[i];
q.push((pnt){arr[i],dis[arr[i]]});
}
}
}
int main() {
Init();
Dijkstra();
printf("%d",dis[V+1]);
return 0;
}