Vexoben
Apr 16, 2018
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=1492
题解
首先应该显然的贪心:每次买入就花完所有的钱,卖出就卖完所有的券。
自然就得到一个O(n^2)的DP:令f[i]为前i天的最大收益,x[i]为第i天所有钱买入股票后A股最大持有数,y[i]为B股持有数。
那么就有:
暴力O(n)转移就是O(n^2)了。
考虑用决策单调性优化这个转移。对于两个状态j,k(f[j]< f[k]),k比j优当且仅当:
从中可以看出符合条件的点(x[j],y[j])会形成一个上凸壳,那么我们用平衡树维护一下凸壳,每次二分出斜率刚好小于-A[i]/B[i]的位置,这题就解决了。
但是平衡树太麻烦,我们可以用cdq分治解决这个问题:
Solve(l,r)是一个转移出[l,r]这段区间中的函数,我们对时间分治,按如下步骤进行:
1、调用Solve(l,mid);
2、用[l,mid]中转移出的状态更新[mid+1,r]中的状态;
3、调用Solve(mid+1,r)。
问题在于步骤二如何进行。假设[l,mid]中的状态已经转移完毕,因为可以用来转移的状态已经确定,[mid+1,r]中的状态转移顺序便无关紧要。我们将他们以-A[i]/B[i]为关键字进行排序,现在用来转移和被转移的状态都已经是单调的,我们就可以在O(n)的时间内处理完所有的转移,和一般的斜率优化无异。
注意每次排序都应该在递归上来时进行归并排序,这样复杂度就是O(n*log(n))
一个奇怪的问题:cmp函数中参数取地址会在BZOJ上CE
#include<cmath>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
const double eps=1e-6;
const int inf=0x3f3f3f3f;
int n,m,st[N];
double a[N],f[N];
struct Pnt {
int tim;
double a,b,r,x,y,k;
}p[N],t[N];
inline bool cmp(Pnt u,Pnt v) {
return u.k>v.k;
}
inline double Slop(Pnt u,Pnt v) {
if (abs(v.r+1)<eps) return -inf;
if (abs(u.x-v.x)<eps) return inf;
return (u.y-v.y)/(u.x-v.x);
}
void Solve(int l,int r) {
if (l==r) {
f[l]=max(f[l],f[l-1]);
p[l].y=f[l]/(p[l].r*p[l].a+p[l].b);
p[l].x=p[l].y*p[l].r;
return;
}
int mid=(l+r)>>1,u=l,v=mid+1;
for (int i=l;i<=r;i++) {
if (p[i].tim<=mid) t[u++]=p[i];
else t[v++]=p[i];
}
for (int i=l;i<=r;i++) p[i]=t[i];
Solve(l,mid);
int top=0,bot=1;
for (int i=l;i<=mid;i++) {
while (top&&Slop(p[st[top-1]],p[st[top]])<Slop(p[st[top-1]],p[i])+eps) --top;
st[++top]=i;
}
st[++top]=0;
for (int i=mid+1;i<=r;i++) {
while (bot<top&&Slop(p[st[bot]],p[st[bot+1]])+eps>p[i].k) ++bot;
f[p[i].tim]=max(f[p[i].tim],p[st[bot]].x*p[i].a+p[st[bot]].y*p[i].b);
}
Solve(mid+1,r);
u=l,v=mid+1;
for(int i=l;i<=r;i++) {
if (v>r) t[i]=p[u++];
else if (u>mid) t[i]=p[v++];
else if((p[u].x<p[v].x||(fabs(p[u].x-p[v].x)<eps&&p[u].y<p[v].y))) t[i]=p[u++];
else t[i]=p[v++];
}
for (int i=l;i<=r;i++) p[i]=t[i];
}
int main() {
scanf("%d%lf",&n,&f[0]);
for (int i=1;i<=n;i++) {
scanf("%lf%lf%lf",&p[i].a,&p[i].b,&p[i].r);
p[i].k=-p[i].a/p[i].b; p[i].tim=i;
}
p[0].r=-1;
sort(p+1,p+n+1,cmp);
Solve(1,n);
printf("%.3lf",f[n]);
return 0;
}
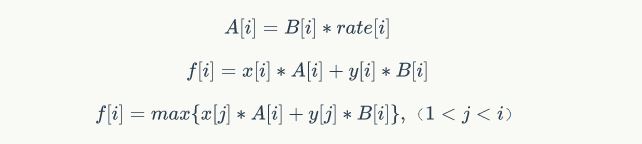
.JPG)